E - Integers on a Tree

Contest Duration: 2016-11-06(Sun) 12:00 - 2016-11-06(Sun) 13:40 (local time) (100 minutes) Back to Home

E - Integers on a Tree Editorial

Time Limit: 2 sec / Memory Limit: 256 MiB

配点 : $800$ 点

問題文

$N$ 頂点の木があり、頂点には $1, 2, ..., N$ と番号が振られています。 $i$ ( $1 ≦ i ≦ N - 1$ ) 番目の辺は頂点 $A_i$ と頂点 $B_i$ を結んでいます。

高橋君は木の $K$ 個の頂点に整数を書き込みました。具体的には、各 $1 ≦ j ≦ K$ について、頂点 $V_j$ に整数 $P_j$ を書き込みました。その後、高橋君は居眠りを始めました。

木を見つけた青木君は、残りのすべての頂点に整数を書き込み、高橋君を驚かせようとしています。高橋君を驚かせるためには、木が次の条件を満たさなければなりません。

条件: 辺で直接結ばれた $2$ つの頂点に書かれている整数の差がちょうど $1$ である。

残りのすべての頂点に書き込む整数を工夫することで、木が条件を満たすようにできるか判定してください。もし可能な場合は、どのように整数を書き込めばよいかを具体的にひとつ求めて下さい。

制約

$1 ≦ N ≦ 10^5$
$1 ≦ K ≦ N$
$1 ≦ A_i, B_i ≦ N$ ( $1 ≦ i ≦ N - 1$ )
$1 ≦ V_j ≦ N$ ( $1 ≦ j ≦ K$ ) (21:18, 制約の誤記を修正)
$0 ≦ P_j ≦ 10^6$ ( $1 ≦ j ≦ K$ )
与えられるグラフは木になることが保証される
$V_j$ はすべて相異なる

入力

入力は以下の形式で標準入力から与えられる。

 $N$ 
 $A_1$   $B_1$ 
 $A_2$   $B_2$ 
 $:$ 
 $A_{N-1}$   $B_{N-1}$ 
 $K$ 
 $V_1$   $P_1$ 
 $V_2$   $P_2$ 
 $:$ 
 $V_K$   $P_K$

出力

残りのすべての頂点に書き込む整数を工夫することで木が条件を満たすようにできるならば Yes を、できないならば No を出力せよ。

条件を満たせる場合、追加で $N$ 行出力せよ。このうちの $v$ ( $1 ≦ v ≦ N$ ) 行目には、頂点 $v$ に書かれる整数を出力せよ。条件を満たすような整数の書き込み方が複数ある場合、そのうちいずれかひとつを出力すればよい。

入力例 1Copy

Copy

出力例 1Copy

Copy

Yes
5
6
6
5
7

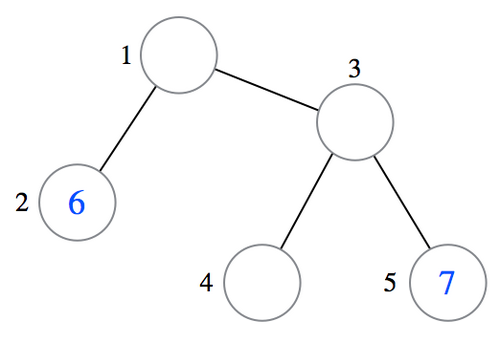
はじめ、木は以下の図のような状態である。頂点のそばに書かれた数が頂点番号を、頂点の中に書かれた青い数が元から書き込まれていた整数を表す。

青木君はたとえば次のように残りの頂点に整数を書き込むことで木が条件を満たすようにできる。これは出力例 $1$ に対応している。

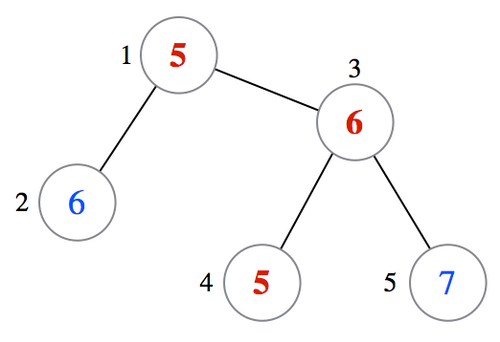
木が条件を満たしていれば、これとは異なった出力でも AC となることに注意せよ。たとえば、入力例 $1$ に対しては

Yes
7
6
8
7
7

という出力でも正答となる。

入力例 2Copy

Copy

出力例 2Copy

Copy

No

入力例 3Copy

Copy

出力例 3Copy

Copy

Yes
0
-1
-2
-3

新たに書き込む整数は負になったり $10^6$ を超えたりしても構わない。

Score : $800$ points

Problem Statement

We have a tree with $N$ vertices. The vertices are numbered $1, 2, ..., N$ . The $i$ -th ( $1 ≦ i ≦ N - 1$ ) edge connects the two vertices $A_i$ and $B_i$ .

Takahashi wrote integers into $K$ of the vertices. Specifically, for each $1 ≦ j ≦ K$ , he wrote the integer $P_j$ into vertex $V_j$ . The remaining vertices are left empty. After that, he got tired and fell asleep.

Then, Aoki appeared. He is trying to surprise Takahashi by writing integers into all empty vertices so that the following condition is satisfied:

Condition: For any two vertices directly connected by an edge, the integers written into these vertices differ by exactly $1$ .

Determine if it is possible to write integers into all empty vertices so that the condition is satisfied. If the answer is positive, find one specific way to satisfy the condition.

Constraints

$1 ≦ N ≦ 10^5$
$1 ≦ K ≦ N$
$1 ≦ A_i, B_i ≦ N$ ( $1 ≦ i ≦ N - 1$ )
$1 ≦ V_j ≦ N$ ( $1 ≦ j ≦ K$ ) (21:18, a mistake in this constraint was corrected)
$0 ≦ P_j ≦ 10^5$ ( $1 ≦ j ≦ K$ )
The given graph is a tree.
All $v_j$ are distinct.

Input

The input is given from Standard Input in the following format:

 $N$ 
 $A_1$   $B_1$ 
 $A_2$   $B_2$ 
 $:$ 
 $A_{N-1}$   $B_{N-1}$ 
 $K$ 
 $V_1$   $P_1$ 
 $V_2$   $P_2$ 
 $:$ 
 $V_K$   $P_K$

Output

If it is possible to write integers into all empty vertices so that the condition is satisfied, print Yes. Otherwise, print No.

If it is possible to satisfy the condition, print $N$ lines in addition. The $v$ -th ( $1 ≦ v ≦ N$ ) of these $N$ lines should contain the integer that should be written into vertex $v$ . If there are multiple ways to satisfy the condition, any of those is accepted.

Sample Input 1Copy

Copy

Sample Output 1Copy

Copy

Yes
5
6
6
5
7

The figure below shows the tree when Takahashi fell asleep. For each vertex, the integer written beside it represents the index of the vertex, and the integer written into the vertex is the integer written by Takahashi.

Aoki can, for example, satisfy the condition by writing integers into the remaining vertices as follows:

This corresponds to Sample Output 1. Note that other outputs that satisfy the condition will also be accepted, such as:

Yes
7
6
8
7
7

Sample Input 2Copy

Copy

Sample Output 2Copy

Copy

No

Sample Input 3Copy

Copy

Sample Output 3Copy

Copy

Yes
0
-1
-2
-3

The integers written by Aoki may be negative or exceed $10^6$ .